
Frequency Response Synthesis - Part 2
Purpose
In this installment, we will continue with our RIAA example, showing the effect of how poles and zeros interact when constructed from chained networks of Rs and Cs without any isolation.
Example 1 Continued - RIAA Network
Recap: here's the response associated with RIAA playback equalization:

And here's the circuit used to produce the RIAA response

Modifications to the response curve:
There are two modifications typically applied to the RIAA response curve. A proposal was made to add a 20Hz pole to the curve. This would roll off the audio below 20Hz to reduce "rumble". The problem with this is that the record manufacturers never boosted recording below 20Hz, so the overall composite curve would be 3dB down at 20Hz. Nevertheless, if you have a lot of rumble in your system, this can improve signal to noise substantially.
The second modification is to include a zero at 50kHz. The thought process being that the recording media will begin rolloff about there anyway, so the response could be "flatter". The problem here is whether the zero should be 50kHz, 40kHz, 60kHz etc. Nevertheless, a considerable number of people prefer the 3.18usec (50kHz) zero added to the system. Lets consider how to do both of these modifications. For the low frequency, let's move up the pole associated with the coupling capacitor C1 to 10Hz. We can do this by changing the value of C1 to 0.033uF. What you will find if you do this is the response at 10Hz will be down about 4 dB and the response at 20Hz will be down almost 2 dB at 20Hz. Such is the interaction with the pole at 50Hz. Actually we can achieve a reasonable compromise by changing R3 to 392k along with the change in C1 to 0.033uF. This keeps the response in the bass region closer to RIAA curve, places the response at 20Hz about -0.8dB, and the response at 10Hz -2.4dB. Also the value of R5 needs to be altered due to the interaction with the 500Hz zero and 2123Hz pole. However, the 50kHz will affect this value the other way, so lets ignore that issue for right now.
For the 50kHz zero, lets consider the fully interacting pole-zero network discussed last time (that is, rather than C2 positioned at the plate of the second tube, it is placed across R5. Remember this caused R5 to change to 27k, and the capacitor in parallel with it was 2.95nF). We can create a zero at 50kHz by placing a resistor in series with that capacitor. A resistor value of 1.58k provides the required attenuation of 47.5dB. When we do this, however, the capacitor needs to change from 2.95nF to 2.7nF. Also the combination of the new LF pole and the new HF zero require a slight alteration of R5 to 27.4k.
If you're thoroughly confused, the schematic now looks like this:

and the achieved frequency response looks like this:
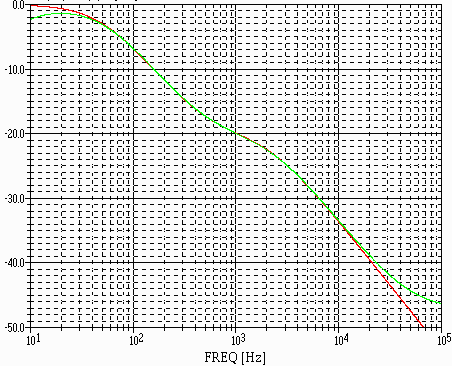
In this case the RED is the standard RIAA curve, and the GREEN is our newly synthesized curve.
In case you're wondering about that R5 value, with ONLY the additional LF pole, R5 would need to be 26.7k, and with ONLY the additional HF zero, R5 would need to be 28k.
Let's summarize: when we added a 10Hz pole to the equation, we needed to move the 50Hz pole to 42 Hz to "compensate" for the interaction. If we were to change this the first pole to 20Hz, we would need to change the 50Hz pole to about 34Hz to compensate. If we were to raise the first pole much further, it would be essentially impossible to "compensate" for the interaction. Notice that a 5:1 ratio in pole frequencies caused about 16% shift in pole position, and a 2.5:1 ratio of pole frequencies caused a 32% shift in the pole position.
Next : Loudness Compensation.
Steve